Stack을 활용해 중위계산법을 구현해보자
중위계산법은 그냥 우리가 생각하는 일반적인 방법이다.
검증 할 식
ex) 10 * 5 - 8 / 4 + 2 * 3
계산을 하기 위해 Stack에 쌓아보자
여기서 구현 할때 String문자를 10진수 변환 하기 위해 strtoul 함수를 사용했다
strtoul을 사용하여 10진수를 바꿔보면 + 부호 - 부호는 같이 묶여서 나타난다.
즉 부호는 * / 만 존재한다.
다음 식을 Stack에 담아 보자
ex) 10 + 9 * 5 * -2 / 1 + 2 * 3

식을 계산 할려면 왼쪽에서 오른쪽으로 읽어가면서 곱셈, 나눗셈이 있는지 확인 해야 하는데 Stack Pointer는 반대 쪽에
위치하고 있다
옮겨 주자
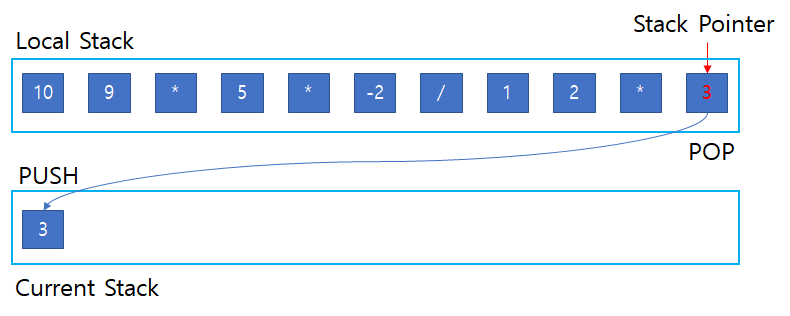
끝까지 옮기면 다음과 같은 그림이 완성 된다.

그림 같이 함수 구현 코드
infix_form 함수
int calc_op_check(int op)
{
switch (op)
{
case '*':
case '/':
return 1;
default:
return -1;
}
}
int infix_form(char *buf, Stack *CurrentStack)
{
int num = 0;
Stack Local_Stack;
StackInit(&Local_Stack);
while (1)
{
num = strtoul(buf, &buf, 10);
if (num != 0)
{
SPush(&Local_Stack, num);
}
else
{
if (calc_op_check(*buf) != -1)
{
SPush(&Local_Stack, *buf);
buf += 1;
}
else
{
printf(" Format OK !! \r\n");
break;
}
}
}
while (Local_Stack.stack_ptr != -1)
SPush(CurrentStack, SPop(&Local_Stack));
return 0;
}
main에 다음과 같이 실행 하면 정상적으로 Stack이 쌓인걸 확인 할 수 있다.
Stack Normal_Stack;
int main(void)
{
StackInit(&Normal_Stack);
char *calc_equal =
{ "10+9*5*-2/1+2*3" };
infix_form(calc_equal, &Normal_Stack);
}실행 결과
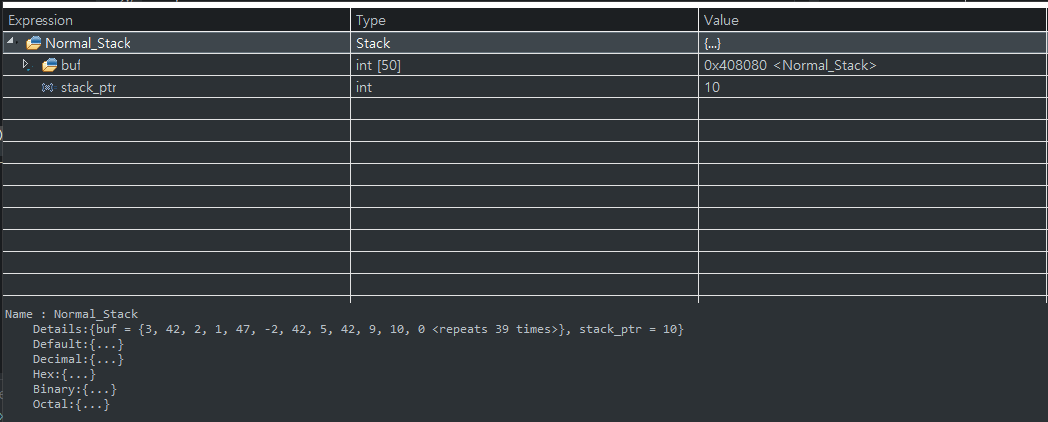
stack pointer 는 10이고 10이 가리키는 숫자는 10인 걸 알 수 있다.
남은 건 이제 Stack에 있는 숫자들을 빼서 계산하면 된다.
int infix_calculator(Stack *LStack)
{
int result = 0;
while (LStack->stack_ptr != 0)
{
result = infix_calc(LStack);
}
return result;
}
계산 방법
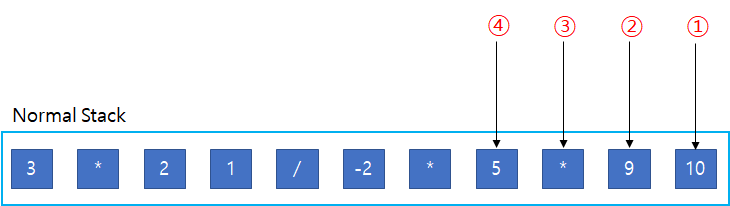
그림과는 다른 데 처음에 언급했던 식을 가지고 한번 계산 해보자
식: 10 * 5 -8 / 4 + 2 * 3
infix_form() 함수로 식을 스택으로 변환 후
스택: 3 *2 4 / -8 5 * 10
↑Stack Pointer
계산과정은 다음과 같다.
1. Stack에 1번을 POP 한다
연산 부호면 에러메시지를 띄우고 종료한다.
2. 1번 경우가 아니라면 Stack의 2번을 POP 한다.
연산 부호면 1번과 3번을 부호에 맞게 계산 후 결과 값을 Stack에 Push 한 후 종료한다..
ex) 2번 부호가 연산 부호인 상황
-> 3 * 2 4 / -8 5 * 10 (연산 전 스택)
-> 3 * 2 4 / -8 50 (연산 후 스택)
3. 2번 경우가 아니라면 Stack의 3번을 POP 한다.
연산 부호면 2번과 4번을 부호에 맞게 계산 후 결과 값을 Stack에 Push 한 후 종료한다.
ex) 3번 부호가 연산 부호인 상황
-> 3 * 2 4 / -8 50 (①: 50, ②:-2, ③: / )
-> 3 * 2 -2 50 (연산 후 스택 ※ Stack에 거꾸로 넣었으므로 계산은 4/-8이 아닌 -8/4가 되어야 한다.)
4. 위 모든 경우가 다 아니라면.....
연산 부호가 없으면 1번과 2번을 더한다.
ex) 3번 부호까지 연산부호가 없는 상황
-> 3 * 2 -2 50 (①: 50, ②:-2, ③: 2)
-> 3 * 2 48 (연산 후 스택)
스택이 1개 남을 때 까지 위 과정을 반복 한다.
해당 구현 코드
Operand_Checkdef Opcode_Check(Stack *LStack)
{
int local_buf_1 = 0;
int local_buf_2 = 0;
/* 1번 경우 */
if (SPeek(LStack) == '/' || SPeek(LStack) == '*')
{
return OPERAND_1;
}
/* 2번 경우 */
local_buf_1 = SPop(LStack);
if (SPeek(LStack) == '/' || SPeek(LStack) == '*')
{
SPush(LStack, local_buf_1);
return OPERAND_2;
}
/* 3번 경우 */
local_buf_2 = SPop(LStack);
if (SPeek(LStack) == '/' || SPeek(LStack) == '*')
{
SPush(LStack, local_buf_2);
SPush(LStack, local_buf_1);
return OPERAND_3;
}
SPush(LStack, local_buf_2);
SPush(LStack, local_buf_1);
return OPERAND_ERR;
}
/*Opcode_Check를 통해 연산자 위치를 확인 하고 확인된 위치에 맞게 계산한다.*/
int infix_calc(Stack *LStack)
{
int operator = 0;
int operand_1 = 0;
int operand_2 = 0;
int operand_3 = 0;
int calc_result = 0;
switch (Opcode_Check(LStack))
{
case OPERAND_1:
printf("calc_equal ERROR !!");
return -1;
case OPERAND_2:
operand_1 = SPop(LStack);
operator = SPop(LStack);
operand_2 = SPop(LStack);
calc_result = multi_div_calc(operator, operand_1, operand_2);
SPush(LStack, calc_result);
break;
case OPERAND_3:
operand_1 = SPop(LStack);
operand_2 = SPop(LStack);
operator = SPop(LStack);
operand_3 = SPop(LStack);
calc_result = multi_div_calc(operator, operand_2, operand_3);
SPush(LStack, calc_result);
SPush(LStack, operand_1);
break;
default:
operand_1 = SPop(LStack);
operand_2 = SPop(LStack);
calc_result = operand_1 + operand_2;
SPush(LStack, calc_result);
return calc_result;
}
return 0xff;
}실행 Main 함수
int main(void)
{
int result;
StackInit(&Normal_Stack);
char *calc_equal =
{ "10*5-8/4+2*3" };
infix_form(calc_equal, &Normal_Stack);
result = infix_calculator(&Normal_Stack);
printf( "calculator result is %d \r\n",result);
return result;
}
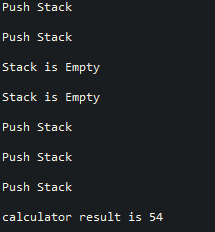
실행 결과
'자료구조' 카테고리의 다른 글
| Stack - 후위표기법 -1(계산) (0) | 2020.11.16 |
|---|---|
| Stack - 후위표기법 -1(변환) (0) | 2020.11.12 |
| STACK 구현 (0) | 2020.10.22 |
| 연결리스트 #2 리스트 추가기능 (0) | 2020.10.16 |
| 연결 리스트 #1 구현 (0) | 2020.10.15 |



